棋盘覆盖问题——分治法
问题描述
有一个 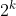
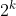

样例:
输入:

输出:

思路——分治法:
将一个规模为n的问题分解为k个规模较小的子问题,这些子问题相互独立且与原问题相同。
递归地解决这些子问题,然后将各个子问题的解合并得到原问题的解。
就是将规模为n的问题自顶向下分解,直到小问题分解到足够小,可以解决时,再自底向上合并,从而得到原来的解。
当k=0(棋盘只有1格),特殊点只能唯一,L骨牌数为0
当k >0,则可将 2*kⅹ2*k 棋盘分割为 4个 2*k-1ⅹ2*k-1 的子棋盘

判断特殊点在哪一个子棋盘中,用一块L骨牌放在其它三个子棋盘的连接处
以此类推,则最后可将每个子棋盘划分为1格的棋盘,结束递归
代码实现:
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 using namespace std; 5 6 int arr[1000][1000]; 7 int num = 0; 8 void ChessBoard(int x, int y, int a, int b, int length); 9 10 int main() { 11 //棋盘大小 12 int length; 13 cout << "请输入length:" ; 14 cin >> length; 15 16 //空白点坐标 17 int a, b; 18 cout << "请输入空格位置:"; 19 cin >> a >> b; 20 cout << endl; 21 22 arr[a][b] = 0;//标点用0表示 23 ChessBoard(1, 1, a, b, length); 24 for (int i = 1; i <= length; i++) { 25 for (int j = 1; j <= length; j++) { 26 cout << arr[i][j] << " "; 27 } 28 cout << endl; 29 } 30 return 0; 31 } 32 33 void ChessBoard(int x, int y, int a, int b, int length) { 34 if (length == 1) { 35 return; 36 } 37 int h = length / 2;//分割棋盘 38 int t = ++num;//骨牌号,从1开始,相同数字代表是同一块 39 40 //以“田”的左下角为(1,1) 41 //左下角 42 if (a < x + h && b < y + h) { 43 ChessBoard(x, y, a, b, h); 44 } 45 else { 46 arr[x + h - 1][y + h - 1] = t; 47 ChessBoard(x, y, x + h - 1, y + h - 1, h); 48 } 49 50 //左上角 51 if (a < x + h && b >= y + h) { 52 ChessBoard(x, y + h, a, b, h); 53 } 54 else { 55 arr[x + h - 1][y + h] = t; 56 ChessBoard(x, y + h, x + h - 1, y + h, h); 57 } 58 59 //右下角 60 if (a >= x + h && b < y + h) { 61 ChessBoard(x + h, y, a, b, h); 62 } 63 else { 64 arr[x + h][y + h - 1] = t; 65 ChessBoard(x + h, y, x + h, y + h - 1, h); 66 } 67 68 //右上角 69 if (a >= x + h && b >= y + h) { 70 ChessBoard(x + h, y + h, a, b, h); 71 } 72 else { 73 arr[x + h][y + h] = t; 74 ChessBoard(x + h, y + h, x + h, y + h, h); 75 } 76 }
参考资料:《计算机算法设计与分析(第四版)》